Before Each Scenario Begins Spheres a B C and D Are Reset to Charges of q 0 Q and 0 Again
Electric Charges and Fields
31 Coulomb's Police force
Learning Objectives
By the end of this section, you lot will exist able to:
- Describe the electric force, both qualitatively and quantitatively
- Calculate the force that charges exert on each other
- Decide the management of the electric force for different source charges
- Correctly describe and apply the superposition principle for multiple source charges
Experiments with electric charges have shown that if two objects each take electric charge, so they exert an electric strength on each other. The magnitude of the force is linearly proportional to the internet charge on each object and inversely proportional to the square of the distance betwixt them. (Interestingly, the force does not depend on the mass of the objects.) The management of the force vector is along the imaginary line joining the two objects and is dictated past the signs of the charges involved.
Let
The electric force ![]() on one of the charges is proportional to the magnitude of its own charge and the magnitude of the other charge, and is inversely proportional to the square of the distance between them:
on one of the charges is proportional to the magnitude of its own charge and the magnitude of the other charge, and is inversely proportional to the square of the distance between them:
![]()
This proportionality becomes an equality with the introduction of a proportionality constant. For reasons that will get clear in a later chapter, the proportionality constant that we use is actually a collection of constants. (We discuss this constant before long.)
Coulomb's Law
The magnitude of the electric force (or Coulomb force) between two electrically charged particles is equal to
![]()
Nosotros apply absolute value signs around the product ![]() considering ane of the charges may be negative, just the magnitude of the force is ever positive. The management of the force vector depends on the sign of the charges. If the charges are the same, the force points abroad from the other charge. If the charges have unlike signs, the force points toward the other charge((Figure)).
considering ane of the charges may be negative, just the magnitude of the force is ever positive. The management of the force vector depends on the sign of the charges. If the charges are the same, the force points abroad from the other charge. If the charges have unlike signs, the force points toward the other charge((Figure)).
It is important to note that the electric forcefulness is not abiding; it is a function of the separation distance between the two charges. If either the exam charge or the source accuse (or both) move, and then ![]() changes, and therefore then does the force. An immediate upshot of this is that direct application of Newton's laws with this force can be mathematically difficult, depending on the specific problem at paw. It can (ordinarily) be washed, but we almost e'er look for easier methods of calculating whatever concrete quantity we are interested in. (Conservation of energy is the most common option.)
changes, and therefore then does the force. An immediate upshot of this is that direct application of Newton's laws with this force can be mathematically difficult, depending on the specific problem at paw. It can (ordinarily) be washed, but we almost e'er look for easier methods of calculating whatever concrete quantity we are interested in. (Conservation of energy is the most common option.)
Finally, the new constant ![]() in Coulomb'southward police force is called the permittivity of complimentary space, or (better) the permittivity of vacuum. It has a very important concrete meaning that we will discuss in a later chapter; for now, information technology is simply an empirical proportionality constant. Its numerical value (to three pregnant figures) turns out to be
in Coulomb'southward police force is called the permittivity of complimentary space, or (better) the permittivity of vacuum. It has a very important concrete meaning that we will discuss in a later chapter; for now, information technology is simply an empirical proportionality constant. Its numerical value (to three pregnant figures) turns out to be
![]()
These units are required to give the force in Coulomb's law the correct units of newtons. Annotation that in Coulomb's law, the permittivity of vacuum is only part of the proportionality constant. For convenience, we often ascertain a Coulomb's constant:
![]()
The Force on the Electron in Hydrogen A hydrogen cantlet consists of a single proton and a single electron. The proton has a charge of ![]() and the electron has
and the electron has ![]() . In the "footing land" of the atom, the electron orbits the proton at most likely distance of
. In the "footing land" of the atom, the electron orbits the proton at most likely distance of ![]() ((Figure)). Calculate the electrical strength on the electron due to the proton.
((Figure)). Calculate the electrical strength on the electron due to the proton.
A schematic delineation of a hydrogen cantlet, showing the force on the electron. This depiction is only to enable us to calculate the force; the hydrogen atom does not really look like this. Recall (Effigy).
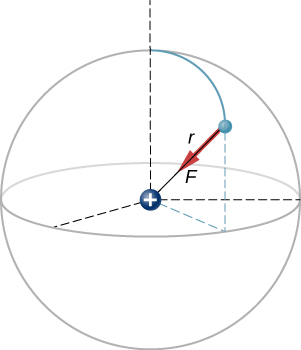
Strategy For the purposes of this example, nosotros are treating the electron and proton as 2 point particles, each with an electric accuse, and we are told the distance betwixt them; we are asked to calculate the strength on the electron. We thus use Coulomb'southward law.
Solution Our two charges and the altitude between them are,
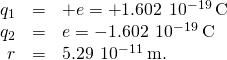
The magnitude of the force on the electron is
![]()
Equally for the management, since the charges on the two particles are opposite, the force is attractive; the force on the electron points radially directly toward the proton, everywhere in the electron's orbit. The force is thus expressed as
![]()
Significance This is a three-dimensional system, and then the electron (and therefore the force on it) can be anywhere in an imaginary spherical beat out around the proton. In this "classical" model of the hydrogen atom, the electrostatic force on the electron points in the inward centripetal management, thus maintaining the electron's orbit. Only note that the quantum mechanical model of hydrogen (discussed in Quantum Mechanics) is utterly dissimilar.
Check Your Agreement What would be different if the electron also had a positive charge?
The force would signal outward.
Multiple Source Charges
The analysis that we have done for two particles can be extended to an arbitrary number of particles; we simply repeat the assay, two charges at a fourth dimension. Specifically, we enquire the question: Given Northward charges (which we refer to as source charge), what is the internet electrical strength that they exert on some other point charge (which we call the test charge)? Annotation that nosotros use these terms considering we tin can think of the test accuse being used to test the forcefulness of the force provided by the source charges.
Like all forces that we have seen up to now, the net electric force on our test charge is simply the vector sum of each individual electric force exerted on it past each of the individual examination charges. Thus, we can summate the net force on the test charge Q by calculating the force on information technology from each source charge, taken one at a time, and then adding all those forces together (as vectors). This ability to simply add up individual forces in this mode is referred to as the principle of superposition, and is 1 of the more of import features of the electrical force. In mathematical form, this becomes
![]()
In this expression, Q represents the charge of the particle that is experiencing the electric force ![]() , and is located at
, and is located at ![]() from the origin; the
from the origin; the ![]() are the N source charges, and the vectors
are the N source charges, and the vectors ![]() are the displacements from the position of the ith accuse to the position of Q. Each of the N unit vectors points directly from its associated source accuse toward the test accuse. All of this is depicted in (Figure). Please note that at that place is no physical difference between Q and
are the displacements from the position of the ith accuse to the position of Q. Each of the N unit vectors points directly from its associated source accuse toward the test accuse. All of this is depicted in (Figure). Please note that at that place is no physical difference between Q and ![]() ; the difference in labels is merely to permit clear discussion, with Q being the accuse nosotros are determining the force on.
; the difference in labels is merely to permit clear discussion, with Q being the accuse nosotros are determining the force on.
The eight source charges each apply a strength on the single examination accuse Q. Each force tin exist calculated independently of the other seven forces. This is the essence of the superposition principle.
(Note that the force vector ![]() does not necessarily point in the aforementioned direction as the unit vector
does not necessarily point in the aforementioned direction as the unit vector ![]() ; it may point in the opposite direction,
; it may point in the opposite direction, ![]() . The signs of the source charge and examination charge determine the direction of the force on the test charge.)
. The signs of the source charge and examination charge determine the direction of the force on the test charge.)
There is a complication, however. Just equally the source charges each exert a strength on the test charge, and so likewise (by Newton's 3rd law) does the test charge exert an equal and opposite force on each of the source charges. As a consequence, each source charge would change position. Nevertheless, by (Effigy), the force on the test accuse is a function of position; thus, as the positions of the source charges change, the net force on the exam charge necessarily changes, which changes the force, which over again changes the positions. Thus, the entire mathematical assay quickly becomes intractable. After, we will learn techniques for handling this situation, simply for now, we make the simplifying assumption that the source charges are fixed in place somehow, and so that their positions are abiding in time. (The test charge is immune to move.) With this restriction in identify, the analysis of charges is known equally electrostatics, where "statics" refers to the constant (that is, static) positions of the source charges and the strength is referred to as an electrostatic force.
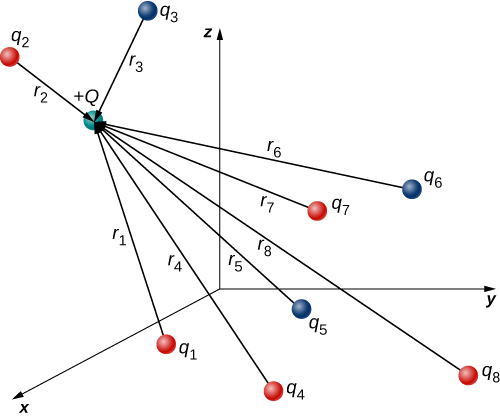
The Internet Force from Two Source Charges Three different, modest charged objects are placed every bit shown in (Figure). The charges ![]() and
and ![]() are fixed in place;
are fixed in place; ![]() is free to move. Given
is free to move. Given ![]() ,
, ![]() , and
, and ![]() , and that
, and that ![]() , what is the internet strength on the heart charge
, what is the internet strength on the heart charge ![]() ?
?
Source charges ![]() and
and ![]() each employ a force on
each employ a force on ![]() .
.
Strategy Nosotros use Coulomb's police again. The manner the question is phrased indicates that ![]() is our test charge, so that
is our test charge, so that ![]() and
and ![]() are source charges. The principle of superposition says that the force on
are source charges. The principle of superposition says that the force on ![]() from each of the other charges is unaffected by the presence of the other accuse. Therefore, we write down the force on
from each of the other charges is unaffected by the presence of the other accuse. Therefore, we write down the force on ![]() from each and add them together every bit vectors.
from each and add them together every bit vectors.
Solution We have two source charges ![]() and
and ![]() a test charge
a test charge ![]() distances
distances ![]() and
and ![]() and we are asked to find a forcefulness. This calls for Coulomb's police and superposition of forces. There are 2 forces:
and we are asked to find a forcefulness. This calls for Coulomb's police and superposition of forces. There are 2 forces:
![]()
We can't add these forces direct considering they don't point in the same direction: ![]() points only in the −x-management, while
points only in the −x-management, while ![]() points just in the +y-direction. The net force is obtained from applying the Pythagorean theorem to its ten– and y-components:
points just in the +y-direction. The net force is obtained from applying the Pythagorean theorem to its ten– and y-components:
![]()
where
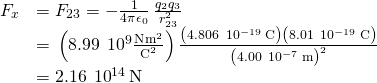
and
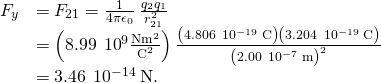
Nosotros find that
![]()
at an angle of
![]()
that is, ![]() above the −ten-axis, every bit shown in the diagram.
above the −ten-axis, every bit shown in the diagram.
Significance Notice that when we substituted the numerical values of the charges, we did not include the negative sign of either ![]() or
or ![]() . Call up that negative signs on vector quantities point a reversal of management of the vector in question. Simply for electric forces, the management of the force is determined by the types (signs) of both interacting charges; we determine the strength directions by because whether the signs of the ii charges are the same or are opposite. If you also include negative signs from negative charges when you substitute numbers, y'all run the risk of mathematically reversing the direction of the force you are calculating. Thus, the safest thing to do is to summate just the magnitude of the strength, using the absolute values of the charges, and determine the directions physically.
. Call up that negative signs on vector quantities point a reversal of management of the vector in question. Simply for electric forces, the management of the force is determined by the types (signs) of both interacting charges; we determine the strength directions by because whether the signs of the ii charges are the same or are opposite. If you also include negative signs from negative charges when you substitute numbers, y'all run the risk of mathematically reversing the direction of the force you are calculating. Thus, the safest thing to do is to summate just the magnitude of the strength, using the absolute values of the charges, and determine the directions physically.
It's also worth noting that the but new concept in this example is how to calculate the electrical forces; everything else (getting the net forcefulness from its components, breaking the forces into their components, finding the management of the internet strength) is the same as force issues you accept done earlier.
Check Your Agreement What would exist different if ![]() were negative?
were negative?
The net forcefulness would indicate ![]() below the −x-centrality.
below the −x-centrality.
Summary
- Coulomb'southward police force gives the magnitude of the force between indicate charges. It is
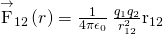
where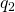 and
and 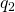 are two point charges separated by a distance r. This Coulomb strength is extremely basic, since virtually charges are due to point-similar particles. Information technology is responsible for all electrostatic effects and underlies nearly macroscopic forces.
are two point charges separated by a distance r. This Coulomb strength is extremely basic, since virtually charges are due to point-similar particles. Information technology is responsible for all electrostatic effects and underlies nearly macroscopic forces.
Conceptual Questions
Would defining the charge on an electron to be positive accept any effect on Coulomb's law?
An atomic nucleus contains positively charged protons and uncharged neutrons. Since nuclei do stay together, what must we conclude nigh the forces between these nuclear particles?
The force belongings the nucleus together must be greater than the electrostatic repulsive force on the protons.
Is the forcefulness between two stock-still charges influenced by the presence of other charges?
Bug
Two point particles with charges ![]() and
and ![]() are held in place by 3-N forces on each charge in appropriate directions. (a) Describe a free-body diagram for each particle. (b) Notice the altitude between the charges.
are held in place by 3-N forces on each charge in appropriate directions. (a) Describe a free-body diagram for each particle. (b) Notice the altitude between the charges.
In a salt crystal, the distance betwixt adjacent sodium and chloride ions is ![]() What is the force of allure between the 2 singly charged ions?
What is the force of allure between the 2 singly charged ions?
Protons in an atomic nucleus are typically ![]() autonomously. What is the electric force of repulsion between nuclear protons?
autonomously. What is the electric force of repulsion between nuclear protons?
![]()
Suppose World and the Moon each carried a net negative charge −Q. Approximate both bodies as point masses and bespeak charges.
(a) What value of Q is required to balance the gravitational allure betwixt Earth and the Moon?
(b) Does the distance between Globe and the Moon touch your respond? Explicate.
(c) How many electrons would be needed to produce this accuse?
Where must ![]() of the preceding problem exist placed then that the net forcefulness on it is zero?
of the preceding problem exist placed then that the net forcefulness on it is zero?
Two small balls, each of mass 5.0 grand, are attached to silk threads 50 cm long, which are in turn tied to the aforementioned point on the ceiling, as shown below. When the assurance are given the same accuse Q, the threads hang at ![]() to the vertical, every bit shown below. What is the magnitude of Q? What are the signs of the two charges?
to the vertical, every bit shown below. What is the magnitude of Q? What are the signs of the two charges?
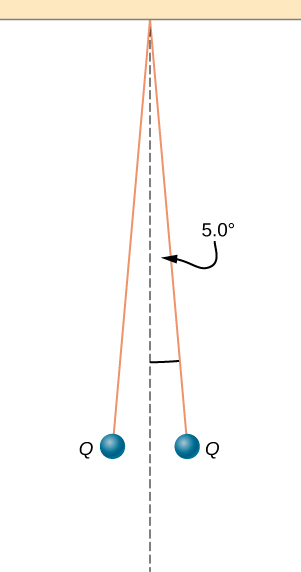
The tension is ![]() . The horizontal component of the tension is
. The horizontal component of the tension is ![]()
![]() .
.
The charges can be positive or negative, but both have to exist the same sign.
The net excess charge on ii small spheres (pocket-size enough to be treated as point charges) is Q. Show that the force of repulsion betwixt the spheres is greatest when each sphere has an excess charge Q/2. Assume that the altitude between the spheres is and then large compared with their radii that the spheres tin be treated as indicate charges.
Let the charge on 1 of the spheres exist nQ, where n is a fraction between 0 and i. In the numerator of Coulomb's constabulary, the term involving the charges is ![]() This is equal to
This is equal to ![]() . Finding the maximum of this term gives
. Finding the maximum of this term gives ![]()
Two small, identical conducting spheres repel each other with a forcefulness of 0.050 North when they are 0.25 m autonomously. Subsequently a conducting wire is connected between the spheres and then removed, they repel each other with a force of 0.060 North. What is the original charge on each sphere?
A charge ![]() is placed at the point P shown below. What is the strength on q?
is placed at the point P shown below. What is the strength on q?
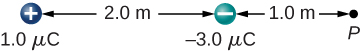
Ascertain right to exist the positive management and hence left is the negative direction, then ![]()
What is the net electric forcefulness on the charge located at the lower right-hand corner of the triangle shown here?

Two fixed particles, each of accuse ![]() are 24 cm apart. What force exercise they exert on a tertiary particle of charge
are 24 cm apart. What force exercise they exert on a tertiary particle of charge ![]() that is 13 cm from each of them?
that is 13 cm from each of them?
The particles form triangle of sides 13, 13, and 24 cm. The x-components abolish, whereas in that location is a contribution to the y-component from both charges 24 cm autonomously. The y-axis passing through the third accuse bisects the 24-cm line, creating ii right triangles of sides 5, 12, and thirteen cm.
![]() in the negative y-management since the force is bonny. The net forcefulness from both charges is
in the negative y-management since the force is bonny. The net forcefulness from both charges is ![]() .
.
The charges ![]() and
and ![]() are placed at the corners of the triangle shown below. What is the forcefulness on
are placed at the corners of the triangle shown below. What is the forcefulness on ![]()
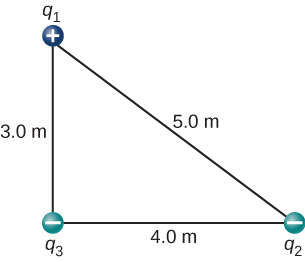
What is the forcefulness on the accuse q at the lower-right-hand corner of the square shown here?
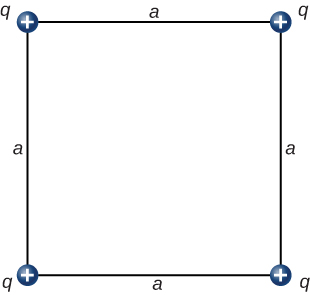
The diagonal is ![]() and the components of the force due to the diagonal charge has a cistron
and the components of the force due to the diagonal charge has a cistron ![]() ;
;
![]()
Glossary
- Coulomb forcefulness
- another term for the electrostatic force
- Coulomb's law
- mathematical equation calculating the electrostatic force vector between ii charged particles
- electrostatic force
- amount and direction of attraction or repulsion between two charged bodies; the assumption is that the source charges remain motionless
- electrostatics
- written report of charged objects which are not in movement
- permittivity of vacuum
- also chosen the permittivity of free space, and constant describing the forcefulness of the electric force in a vacuum
- principle of superposition
- useful fact that we can simply add upwardly all of the forces due to charges acting on an object
tysonansitionve35.blogspot.com
Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/coulombs-law/
0 Response to "Before Each Scenario Begins Spheres a B C and D Are Reset to Charges of q 0 Q and 0 Again"
Post a Comment